REED: Calculating Power After Estimation – Everybody Should Do This!
So your estimate is statistically insignificant and you’re wondering: Is it because the effect size is small, or does my study have too little power? In Tian et al. (2024), we propose a simple method for calculating statistical power after estimation (“post hoc power analysis”). While our application is targeted towards empirical studies in development economics, the method has many uses and is widely applicable across disciplines.
It is common to calculate statistical power before estimation (“a priori power analysis”). This allows researchers to determine the minimum sample size to achieve a given level of power for a given effect size. In contrast, post hoc power analysis is rarely done, and often discouraged (for example, see here).
There is a reason for this. The most common method for calculating post hoc power is flawed. In our paper, we explain the problem and demonstrate that our method successfully avoids this issue.
Before discussing our method, it is useful to review some of the reasons why one would want to calculate statistical power after estimation is completed.
When estimates are insignificant. All too commonly, statistical insignificance is taken as an indication that the true effect size is small, indistinguishable from zero. That may be the case. But it also may be the case that the statistical power of the study was insufficient to generate significance even if the true effect size were substantial. Knowing the statistical power of the regression equation that produced the estimated effect can help disentangle these two cases.
When estimates are significant. Post hoc power analysis can also be useful when estimates are statistically significant. In a recent paper, [Ioannidis et al. (2017)](http://The Power of Bias in Economics Research) analyzed “159 empirical economics literatures that draw upon 64,076 estimates of economic parameters reported in more than 6,700 empirical studies”. They calculated that the “median statistical power is 18%, or less.” Yet the great majority of these estimates were statistically significant. How can that be?
One explanation is Type M error. As elaborated in Gelman and Carlin (2014), Type M error is a phenomenon associated with random sampling . Estimated effects that are statistically significant will tend to be systematically larger than the population effect. If journals filter out insignificant estimates, then the estimates that get published are likely to overestimate the true effects.
Low statistical power is an indicator that Type M error may be present. Post hoc power analysis cannot definitively establish the presence of Type M error. The true effect may be substantially larger than the value assumed in the power analysis. But post hoc power analysis provides additional information that can help the researcher interpret the validity of estimates.
Our paper provide examples from actual randomized controlled trials that illustrate the cases above. We also demonstrate how post hoc power analysis can be useful to funding agencies to assess whether previously funded research met their stated power criteria.
Calculating statistical power. Mathematically, the calculation of statistical power (either a priori or post hoc) is straightforward. Let:
ES = an effect size
s.d.(ES_hat) = the standard deviation of estimated effects, ES_hat
τ = ES / s.d.(ES_hat)
tcritdf,1-α/2 = the critical t-value for a two-tailed t-test having df degrees of freedom and an associated significance level of α.
Given the above, one can use the equation below to calculate the power associated with any effect size ES:
(1) tvaluedf,1-Power = (tcritdf,1-α/2 – τ )
Equation (1) identifies the area of the t-distribution with df degrees of freedom that lies to the right of (tcritdf,1-α/2 – τ) (see FIGURE 1 in Tian et al., 2024). All that is required to calculate power is a given value for the effect size, ES; the standard deviation of estimated effect sizes, s.d.(ES_hat), which will depend on the estimator (e.g., OLS, OLS with clustered standard errors, etc.); the degrees of freedom df and the significance level α.
Most software packages that calculate statistical power essentially consist of estimating s.d.(ES_hat) based on inputs such as sample size, estimate of the standard deviation of the output variable, and other parameters of the estimation environment. This raises the question, why not directly estimate s.d.(ES_hat) with the standard error of the associated regression coefficient?
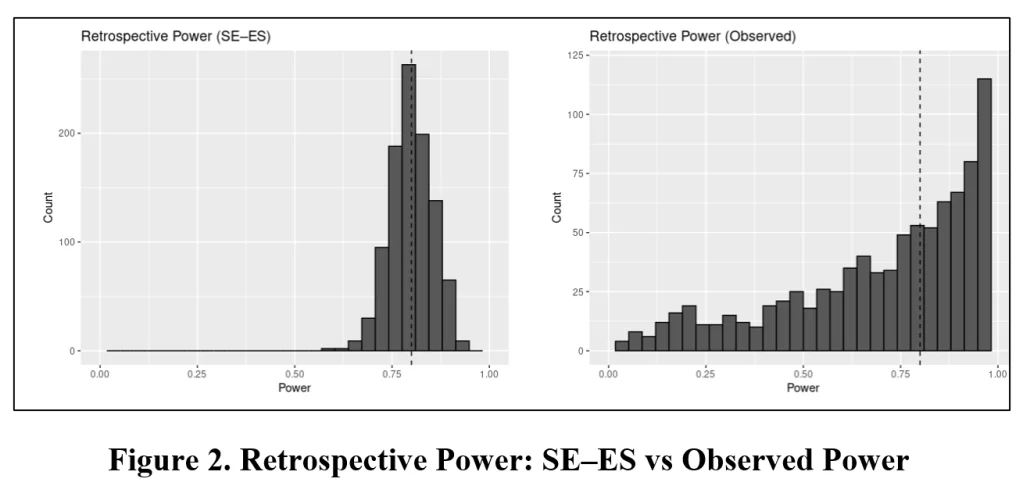
The SE-ES Method. We show that simply replacing s.d.(ES_hat) with the standard error of the estimated effect from the regression equation, s.e.(ES_hat), produces a useful, post hoc estimator of power. We call our method “SE-ES”, for Standard Error-Effect Size.
As long as s.e.(ES_hat) provides a reliable estimate of the variation in estimated effect sizes, SE-ES estimates of statistical power will perform well. As McKenzie and Ozier (2019) note, this condition generally appears to be the case.
Our paper provides a variety of Monte Carlo experiments to demonstrate the performance of the SE-ES method when (i) errors are independent and homoskedastic, and (ii) when they are clustered.
In the remainder of this blog, I present two simple R programs for calculating power after estimation. The first program produces a single-valued, post hoc estimate of statistical power. The user provides a given effect size, an alpha level, and the standard error of the estimated effect from the regression equation along with its degrees of freedom. This program is given below.
# Function to calculate power
power_function <- function(effect_size, standard_error, df, alpha) {
# This matches FIGURE 1 in Tian et al. (2024)
# "Power to the researchers: Calculating power after estimation"
# Review of Development Economics
# http://doi.org/10.1111/rode.13130
t_crit <- qt(alpha / 2, df, lower.tail = FALSE)
tau <- effect_size / standard_error
t_value = t_crit - tau
calculate_power <- pt(t_value, df, lower.tail = FALSE)
return(calculate_power)
}
For example, if after running the power_function above, one wanted to calculate post hoc power for an effect size = 4, given a regression equation with 50 degrees of freedom where the associated coefficient had a standard error of 1.5, one would then run the chunk below.
# Example
alpha <- 0.05
df <- 50
effect_size <- 4
standard_error <- 1.5
power <- power_function(effect_size, standard_error, df, alpha)
print(power)
In this case, post hoc power is calculated to be 74.3% (see screen shot below).
Alternatively, rather than calculating a single power value, one might find it more useful to generate a power curve. To do that, you would first run the following program defining two functions: (i) the power_function (same as above), and (ii) the power_curve_function.
# Define the power function
power_function <- function(effect_size, standard_error, df, alpha) {
# Calculate the critical t-value for the upper tail
t_crit <- qt(alpha / 2, df, lower.tail = FALSE)
qt(alpha / 2, df, lower.tail = FALSE)
tau <- effect_size / standard_error
t_value <- t_crit - tau
calculate_power <- pt(t_value, df, lower.tail = FALSE)
return(calculate_power)
}
# Define the power_curve_function
# Note that this uses the power_function above
power_curve_function <- function(max_effect_size, standard_error, df, alpha) {
# Initialize vector to store results
powers <- numeric(51)
# Calculate step size for incrementing effect sizes
d <- max_effect_size / 50
# Create a sequence of 51 effect sizes
# Each incremented by step size d
effect_sizes <- seq(0, max_effect_size, by = d)
# Loop through each effect size to calculate power
for (i in 1:51) {
effect_size <- effect_sizes[i]
power_calculation <- power_function(effect_size, standard_error, df, alpha)
powers[i] <- power_calculation
}
return(data.frame(EffectSize = effect_sizes, Power = powers))
}
Now suppose one wanted to create a power curve that corresponded to the previous example. You would still have to set alpha and provide values for df and the standard error from the estimated regression equation. But to generate a curve, you would also have to specify a maximum effect size.
The code below sets a maximum effect size of 10, and then creates a sequence of effect sizes from 0 to 10 in 50 equal steps.
# Define global parameters
alpha <- 0.05
df <- 50
standard_error <- 1.5
max_effect_size <- 10
d <- max_effect_size / 50
effect_sizes <- seq(0, max_effect_size, by = d)
Running the chunk below generates the power curve.
# Calculates vector to hold power values
powers <- numeric(51)
# Loop through each effect size to calculate power
for (i in 1:51) {
effect_size <- effect_sizes[i]
power_calculation <- power_function(effect_size, standard_error, df, alpha)
powers[i] <- power_calculation
}
# Generate power curve data
power_data <- power_curve_function(max_effect_size, standard_error, df, alpha)
# Plot power curve
ggplot(power_data, aes(x = EffectSize, y = Power)) +
geom_line() +
labs(title = "Power Curve", x = "Effect Size", y = "Power") +
theme_minimal()
# This shows the table of power values for each effect size
View(power_data)
The power curve is given below.
The last line of the chunk produces a dataframe that lists all the effect size-power value pairs. From there one can see that given a standard error of 1.5, the associated regression equation has an 80% probability of producing a statistically significant estimate when the effect size = 4.3.
The code above allows one to calculate power values and power curves for one’s own research. But perhaps its greatest value is that it allows one to conduct post hoc power analyses of estimated effects from other studies. All one needs to supply the programs is the standard error of the estimated effect and the associated degrees of freedom.
Limitation. The performance of the SE-ES method depends on the nature of the data and the type of estimator used for estimation. We found that it performed well when estimating linear models with clustered errors. However, one should be careful in applying the method to settings that are different from those investigated in our experiments. Accordingly, good practice would customize Tian et al.’s (2024) Monte Carlo simulations to see if the results carry over to data environments that represent the data at hand. To facilitate that, we have provided the respective codes and posted them at OSF here.
NOTE: Bob Reed is Professor of Economics and the Director of UCMetaat the University of Canterbury.He can be reached at bob.reed@canterbury.ac.nz.
REFERENCE
Tian, J., Coupé, T., Khatua, S., Reed, W. R., & Wood, B. D. K. (2024). Power to the researchers: Calculating power after estimation. Review of Development Economics, 1–35. https://doi.org/10.1111/rode.13130
Share this:
- Click to share on X (Opens in new window) X
- Click to share on Facebook (Opens in new window) Facebook
Like Loading…